Introduction

The purpose of this paper is to reassess movements in prices and other economic indicators in Roman Egypt during the period up to AD 270. The start of the period, AD 1, has been chosen to allow for a suitable period of consolidation of Roman as opposed to prior Ptolemaic practices to have taken place following Augustus’s conquest of Egypt in 30 BC. However, in practice, we lack the data to arrive at any firm conclusions for the period prior to AD 50. The endpoint of AD 270 was chosen to avoid the distortion caused by the jump in prices in the 270s when there was a ‘brusque leap in price levels around 274 by a factor of ten or more’ (Rathbone 1997: 215). The paper seeks to test the accepted view, based on Rathbone’s papers (Rathbone 1997; Rathbone and von Reden 2014), that the ‘distribution of prices of particularly well-documented goods — wheat, wine, and donkeys — points to the existence of two distinct periods of price stability, from the late first century CE to the 160s CE or a bit later and from the 190s to the early 270s CE’ (Scheidel 2010: 428). This is repeated as ‘there is also Rathbone’s study of Egyptian prices, the only useable series from anywhere in the Empire, which sees the doubling between A.D. 160 and 190 as the only significant change between A.D. 45 and A.D. 274/5’ (Howgego et al. 2010: 1).1 This view of static prices up to AD 274 was restated recently (Cuvigny and Lach-Urgacz 2020: 321, n 35) ‘as is well known, inflation starts in 274’. This paper concludes that the accepted view is largely correct for wheat, but that other prices are likely to have continued to increase in the period after AD 190.

This paper sits firmly within the wider context of academic interest in the quantification of the Roman economy, exemplified by the OxREP (Oxford Roman Economy Project) and SDEP (Structural Determinants of Economic Performance in the Roman World) programmes in Oxford and Flanders respectively. It also sits within the debate on the nature of money and coinage in the Roman world and their relation to prices (see Elliott 2020 for discussion of the theories and the evidence particularly in relation to coinage debasement). As noted above, Roman Egypt is the only location where there is sufficient data to assess price inflation and thus has often been used as a proxy for inflation throughout the Roman world, and a clear understanding of inflationary trends is a necessary pre-requisite for works dealing with fiscal policy, real income trends or economic growth and decline over the period. It is unashamedly quantitative in its approach and seeks to use mathematical tools to assess trends rather than rely on historical or anecdotal evidence.

In any study of price developments over time, it is essential that the data for each good, asset, or service is as homogenous as possible to enable valid comparisons to be made. This homogeneity naturally includes the geographical source of the data and we must try to avoid distortion of the data caused by regional variations. We are fortunate that the available data for commoditised goods such as wine and cereals, and services, essentially comes from Middle Egypt alone, and with the exceptional transport links supplied by the Nile, any regional variations will have been minimised. For capital assets such as land and housing I have limited the data analysed to local administrative areas or ‘nomes’.

The structure of this paper is broadly as follows: the next section deals with the methodology used to collect commodity prices or other indicators and to analyse them. Then, the resultant patterns are displayed to see if trends can be identified. In the following section, the price data from individual commodities are combined into a ‘blended’ price index, weighted by the number of observations for each component, to allow a general inflationary measure to be determined. In the final section, conclusions are drawn. The appendices provide comments on the data for specific commodities and indicators and list the references concerned.2

Methodology

This paper deals with inflation in the sense of rising prices of commodities or goods, which reduce the purchasing power of each unit of currency over time, as each unit purchases fewer such goods. It should be stressed that this paper deals with nominal prices expressed in the units of currency rather than prices based on the intrinsic metallic value of coinage. I believe that this is the appropriate approach for the period concerned given the relatively low levels of nominal price growth and would have reflected the actual perception of individuals in the marketplace using the available coinage. If inflation were very high then an alternative approach would need to be adopted, using logarithmic plotting of nominal prices (as was adopted by Mickwitz as early as 1932) or restatement of nominal prices into metallic equivalents (as used in Bagnall 1985 for the fourth century and see also Bagnall and Bransbourg 2020). I have not adopted any adjustments for coinage debasement in my analysis since my ambitions in preparing this paper are limited to demonstrating the nominal price trend information so as to allow this to be made available to other scholars in the hope that it will influence their work.

Methodology used for individual commodities and other indicators

A three-stage process was undertaken in relation to data-gathering. Firstly, a normative database of all documentary papyri was established. Then from within this wider database, the transactions of interest were identified and listed in separate databases. Transactions of interest might either be prices of goods themselves which might be included in a consumption basket for measuring inflation (barley, donkeys, wheat, wine) or economic indicators, which may reasonably be expected to have a relationship with price inflation. Those indicators where sufficient data exist to allow analysis are donkey rents, earnings, house prices/rents, land prices/rents, loan sizes, and slave prices. Note that these indicators may not be expected to have a ‘one to one’ relationship with commodity prices but may be expected to follow similar patterns over the medium to long term. Thus, they are more useful for indicating the shape and medium-term timing of increases than the absolute amount of such inflation. Finally, the relevant information was extracted for each transaction and populated within the relevant database.

The first task was thus to establish a normative database against which theories could be tested. The database from which the data were collected is the Duke Databank of Documentary Papyri (DDbDP), as set out within papyri.info, including most published papyri collections.3 Whilst, as noted by van Minnen, no database can be regarded as covering all the relevant papyri in existence and there may be published documentary papyri which have been omitted, the vast bulk of published papyri are included within the DDbDP (van Minnen 2009: 652). The total number of documents examined was 18,962 and the diachronic and geographical distributions were analysed to identify where bias within the data may have existed (see Kelly 2020: 20–28). It should be noted, for instance, that we have few papyri from Alexandria and that the bulk of the papyri from the Oxyrhynchite nome come from the nome capital – Oxyrhynchus.

The normative database provided an initial list of the documents which are particularly relevant to this paper: commodity sales, donkey rents, land sales, house sales, loans and deposits, land leases, and house leases. Searches of papyri.info on key Greek words such as daneion or chresis (loan), hypotheke (mortgage) or phoros (rent) were undertaken and cross-referenced against the lists from the normative database. A physical review of all the published volumes of ostraca and papyri was also made to check no documents had been missed.4 Thereafter, the secondary literature which provides lists of transactions was cross-referenced to ensure that the possibility that a relevant source may have been missed was reduced. The resulting list of documents of particular interest was placed within excel databases. Having identified that a document was of interest, its transcription in papyri.info and the published text were reviewed to identify what details they contained.

Lists of commodity sales, donkey rents, earnings, and financial transactions were thus established as databases. The third process, the population of the databases, differed according to the availability of data within previous scholarship. For commodity prices, donkey rents, and earnings, sufficient data on the prices and the dates was generally available within previous collections. The process here, therefore, was to check the list of identified transactions against the collection to identify any missing transactions, extract the relevant data from the collection, and check it against the primary data within the ostraca and papyri for sense and consistency.5 In practice, the data for commodity prices in this paper naturally have a great commonality with existing collections. However, some additions are mentioned in appendix I, which also lists the collections used and provides commentary on issues specific to a particular good or indicator. For financial transactions relating to loans and real estate, none of the pre-existing collections was sufficiently up to date, comprehensive as to its scope, or contained all the relevant data required to assess prices. The primary works used for cross-referencing of financial transactions were Bogaert 2000; Drexhage 1991; Gendy 1990; Harper 2016; Hennig 1967; Herrmann 1958; Johnson 1936; Kutzner 1989; Lerouxel 2016; Maehler 1983; Masciadri and Montevecchi 1984; Montevecchi 1941 and 1943; Rowlandson 1996; and Tenger 1993.

Given the issues with these previous collections, a different approach was required to investigate the 2,941 financial documents identified as being of interest. This approach was to extract the data from the primary sources and then to check it against the previous collections as opposed to the inverse approach used for the non-financial transactions. In total 4,367 financial transactions were included in these databases which covered land sales, house sales, loans and deposits, land leases, and house leases. I make no claims that the databases thus established are completely exhaustive since human error inevitably means that some documents may be missed or misclassified. I hope, however, that the systematic process undertaken will have eliminated any unconscious bias in the identification of the documents of particular interest and ensured that the vast bulk of relevant transactions will have been included.

Having identified and collected the data, they needed to be analysed. The database format had been chosen as a set of inter-connected excel spreadsheets so as to make this analysis process as easy as possible. Using a spreadsheet allowed medians, averages, and other attributes of the data such as distributions to be relatively easily calculated and displayed. Constructing time series for each of the different variables has challenges related to ensuring that the data are homogenous so that a like for like comparison is made. Performing an analysis of wheat or barley prices is relatively straightforward since wheat and barley were generally priced by the artaba volume measure. Wine is somewhat more problematic since there are various wine measures and there may have been regional variations (Kruit and Worp 1999). The variation in age, sex, and condition of donkeys and slaves means that inevitably the data for these commodities will be more heterogeneous. For donkeys, I have included all donkey sales irrespective of the age of the donkey given the fact that donkeys mature quickly and thus even a young donkey would have commercial value. Children take longer to mature than donkeys and thus for slaves I have looked at data excluding and including children to see whether the results vary. Land prices and rents are those per aroura, and housing data take a whole house as the unit reviewed, whilst to increase homogeneity, only Oxyrhynchite land and Arsinoite housing sales have been used.6 All other commodities and indicators include data from lower and middle Egypt. Earnings are those for unskilled work per day for an adult male. For all commodities and indicators, I have included all relevant data points including those which are not definite, given that it is reasonable to include probable prices rather than ignore them.

Given that this study is concerned with diachronic changes, it has been necessary to ignore data that cannot be adequately dated to a period of time within a range of plus or minus 25 years. I have thus only included data that can be dated to within a 50 year period. So, for example, the donkey price in P.Oxy. XXXVIII 2846, which is dated to the second half of the first century, has been included in the analysis, but that in P.Oslo III 134 which can only be dated to sometime in the third century has been ignored. Imprecisely dated documents have been assumed to be at the mid-point of the date range concerned, thus P.Oxy. XXXVIII 2846 is assumed to date from AD 75.

The approach of using a single date for each source differs from that of Rathbone, who used widely dated data, e.g. ‘“second- or third-century” prices at 190’, when presenting the information in scatter point graph form, but who also helpfully provided an identifier to indicate if a date or price is uncertain (Rathbone 1997: 186). There are advantages and disadvantages to both approaches. Rathbone’s approach makes full use of the available data and allows the reader to form their own opinion from the pattern of points. This runs the risk that, by leaving room for individual judgement, the viewer will see, as in a ‘Rorschach’ ink-blot test, what best suits their preconceptions (Exner 2002). For example, if consumers are seeking to identify the effects of the Antonine plague, the third-century political crises, or coinage debasement, they may be able to convince themselves that they see a suitable pattern (Rathbone 1997: 186). However, restricting the data to sources that can be dated to a relatively short timeframe suits my approach which seeks to identify a best-fit regression line. This line links the points and may then be used to identify numerical values for average inflation of individual commodities and combined into a general index. Duncan-Jones did this on a limited scale by seeing what straight line would best fit the price data he had available for the period AD 100 to 220 but this may hide price developments in the interim since it assumes that inflation is constant over the period (Duncan-Jones 1994: 28). More recently, Harper has adopted a segmented approach and looked at straight-line best-fits for two separate periods for wheat only: the period to AD 160 and from the late second century to AD 275 (Harper 2016: 816).

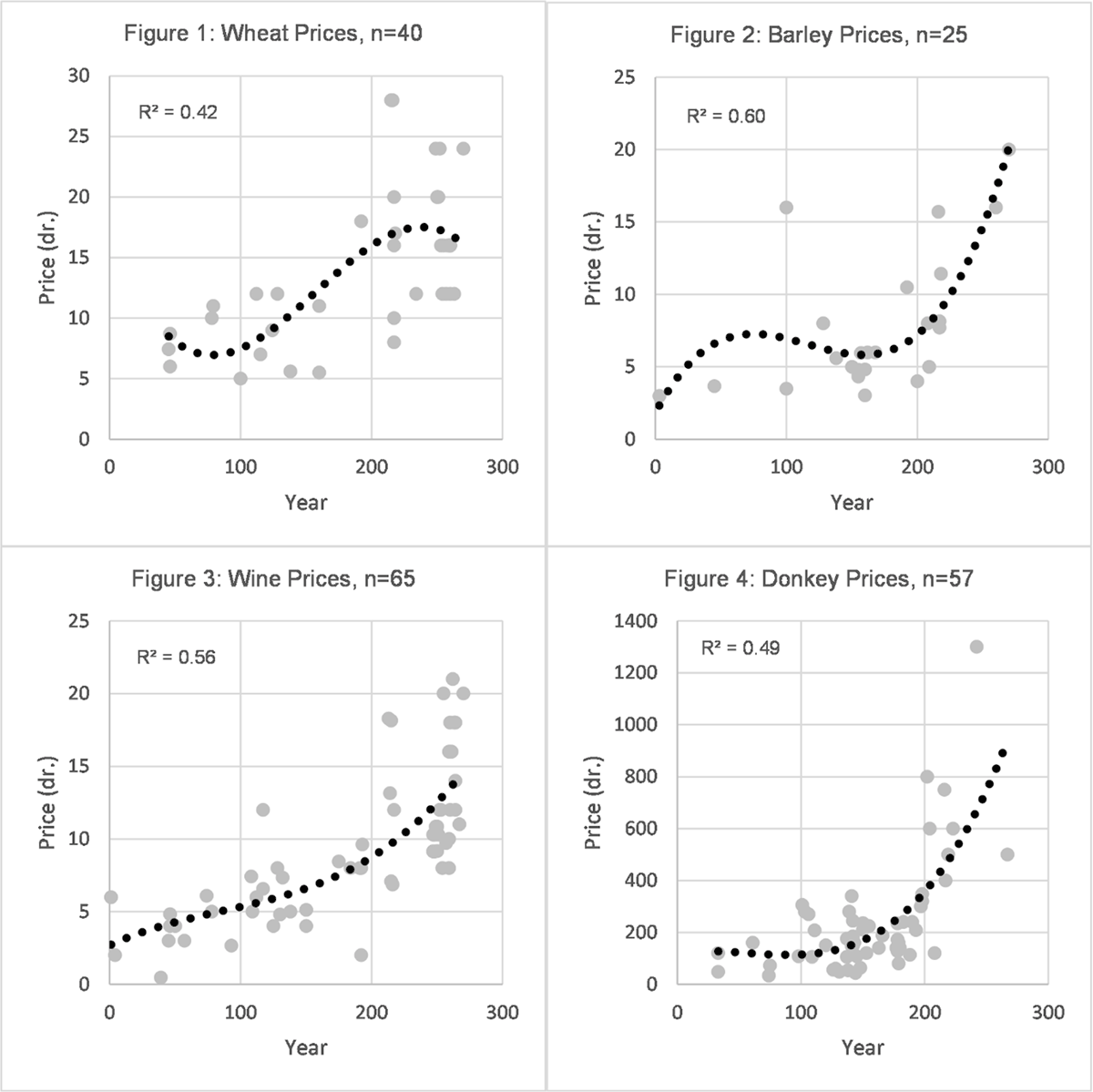
I believe it preferable to use a more nuanced regression line approach that fits the spread of data to a non-linear curve, technically a third-order polynomial which can exhibit two points of inflection, as seen in Figure 1 below for wheat.7 The main reason why this approach is appropriate in these circumstances is that the currently accepted view for price trends assumes just such a curve, with a first point of inflection around AD 160 when prices start to rise and a second point around AD 190 when prices level off. Since the purpose of this paper is to challenge this view, and at least three orders are required in the assessment of these trends, my preference is to use the fewest orders possible on the grounds of simplicity and the limitations of the data. This approach also avoids the need to make subjective assumptions as to the start and end dates of trends which is required if a straight-line or logarithmic regression were adopted.

Figures 1–4
Figures 1–4

Individual commodity prices of wheat, barley, wine, and donkeys from AD 1 to 270. For each graph, the points represent individual observations and a third order polynomial best-fit line is shown in addition to its R2 coefficient.

In a number of documents, prices are given for the same commodity during the same year. For instance in Kronion’s grapheion register P.Mich. II 123 there are some thirteen prices of an artaba of wheat for various months in AD 45 ranging from 2.5 to 4.83 drachmas. For the purposes of this analysis, the data from P.Mich. II 123 for AD 45 are treated as a single point with a median value of 3.0 drachmas per artaba.8 The use of medians reduces some of the sample bias or dependence impacts but it should be noted that it does not eliminate the reliance on documents from the Kronion and Heroninos archives noted by Rathbone (Rathbone 1997: 185).9 We should also remember that there are little or no data from the major city of Alexandria and that for wheat, barley, and wine no data from upper Egypt have been included.

One final word on methodology relates to the monetary denominations. The vast majority of the denominations used, whether units of account or coinage, relate to the Egyptian talents, drachmas, obols, and chalki.10 It is fortunate that for the period under consideration there is a common nominal currency for most of the transactions we are dealing with. In coinage, the silver drachma was normally traded using the Alexandrian billon silver tetradrachm coin which had a value of four drachmas and this explains the tendency which we will see in the transactions for amounts to be in multiples of four, e.g. 24, 28 drachmas etc. For large amounts, these were often expressed in talents, which were each equal to 6,000 silver drachmas. As regards fractions of drachmas, although the exact nature of the relationship between the drachma and obol is complex (see Blouin and Burnett 2020: 255–261), I have converted where possible all values to the Alexandrian silver drachma standard generally using seven obols to the silver drachma after AD 190 and six obols per drachma for the earlier part of the period unless there is evidence to the contrary (Rathbone 1997: 189–190). The obol could further be divided into chalki and eight chalki are assumed per obol.11

Patterns in Commodity Prices and Price Indicators

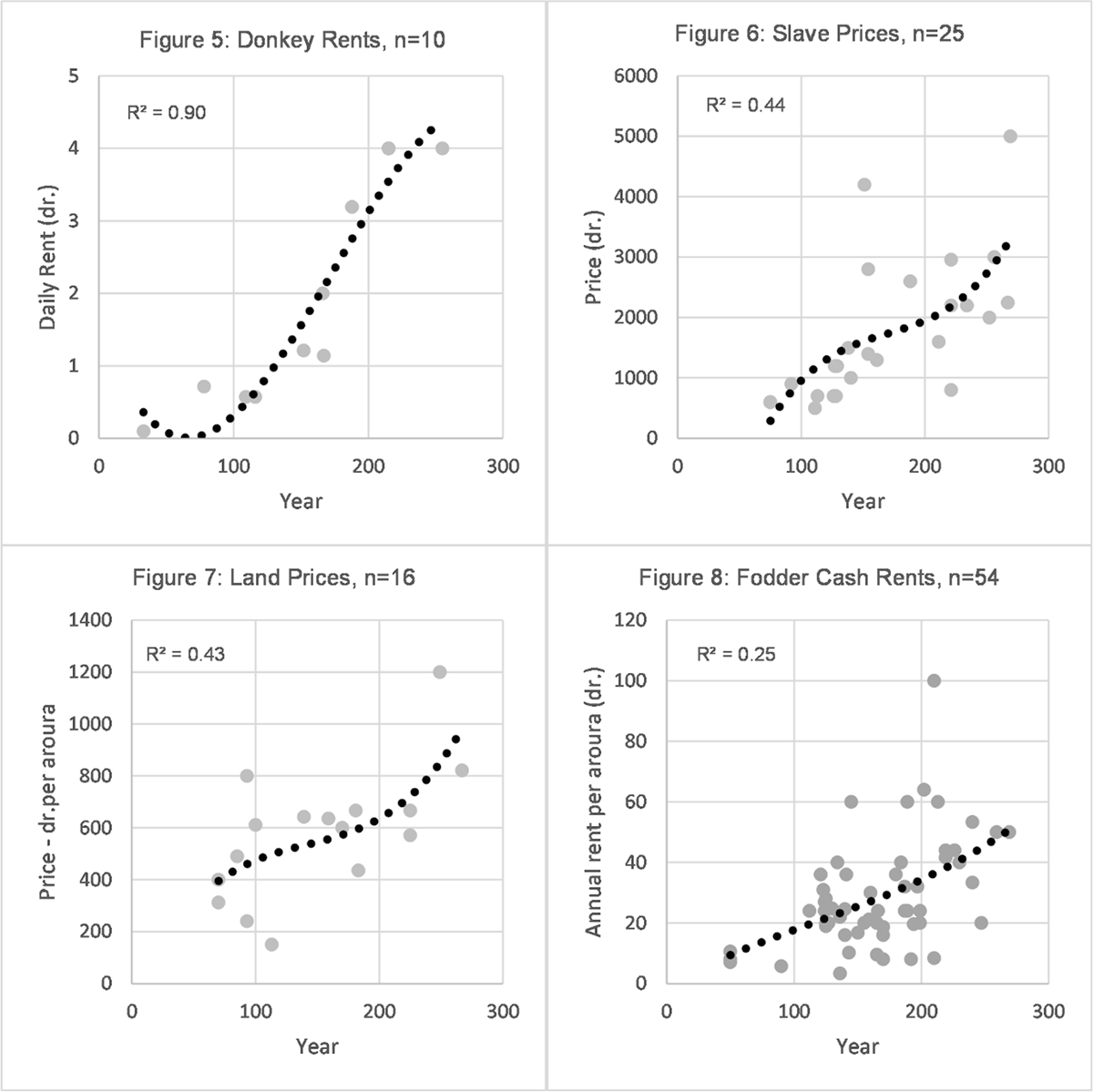
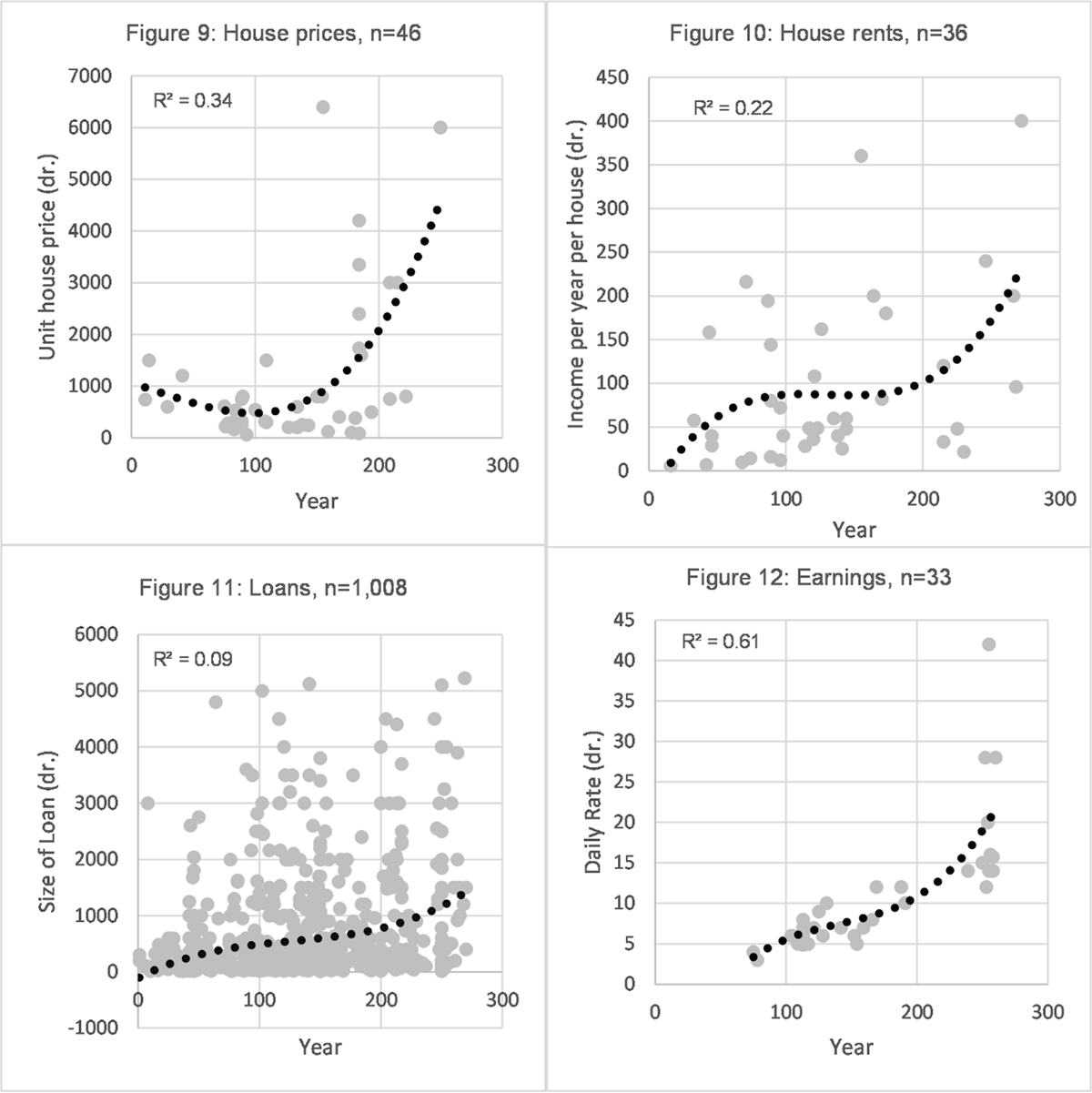
When dealing with multiple time series with relatively few data points it is exceptionally difficult to associate specific probabilities with a proposition that a common trend does or does not exist. It is even more difficult, indeed I believe impossible, to combine findings for different commodities and price indicators to arrive at a statistically valid single probability that generally prices did or did not increase. I have therefore taken the approach to work from the patterns and shapes of best-fit lines through the whole period under consideration in order to test whether the accepted view of inflation is correct.12 When we look for patterns within the curves and statistics shown below we must be aware that, given the small number of observations and the non-chronological price variations that will have existed in our data as a result of regional or other differences, the curves cannot represent fluctuations in prices over the short term. There will have been short-term price differences caused by good and poor harvests, or political and monetary events, and a curve simply represents a smoothed indication of price levels over the longer term. Given these provisos, the development over time of prices and their associated indicators are shown in the charts below (Figures 1–4, 5–8, 9–12). The R2 coefficient shown in each chart is an indicator of the degree of fit of the data to the line drawn.13

Figures 5–8
Figures 5–8

Individual graphs of donkey rents, slave prices, land prices and cash rents for land under fodder from AD 1 to 270. For each graph, the points represent individual observations and a third order polynomial best-fit line is shown in addition to its R2 coefficient.

Figures 9–12
Figures 9–12

Individual graphs of house prices, house rents, loan amounts and daily manual earnings from AD 1 to 270. For each graph, the points represent individual observations and a third order polynomial best-fit line is shown in addition to its R2 coefficient.

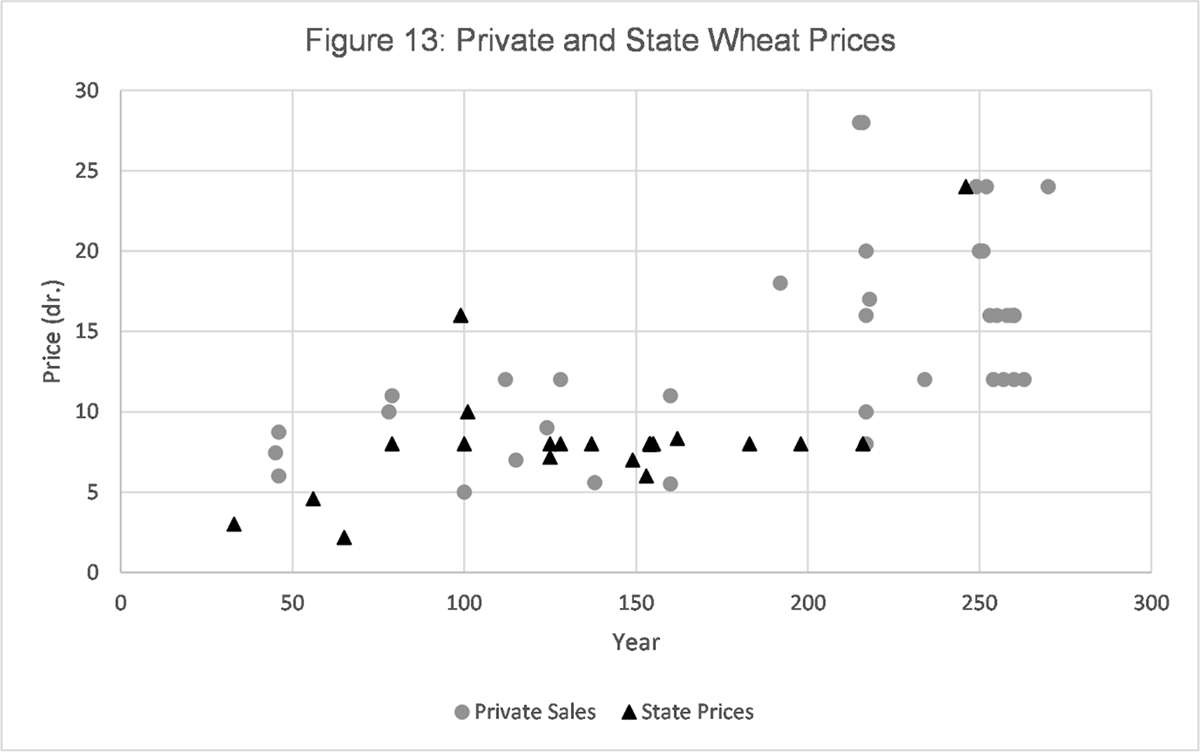
A visual comparison of the best-fit lines shows that there are different patterns for the first century AD, although the prices of goods are generally flat. All the charts show increases from the middle of the second century and thus far the accepted view is validated. However, all the commodities and economic indicators, other than wheat, show increases that do not stop after AD 190 but continue into the third century which is contrary to the accepted view. The best-fit line for wheat, however, is largely consistent with Rathbone’s conclusion that there were two periods of price stability for wheat: up to AD 160 and from AD 190 to 274 with a doubling of prices in the interim. This conclusion is confirmed by examination of the trends from AD 190 for each of the goods concerned on a logarithmically transformed basis, where wheat shows no upward trend, but all other goods do so, although the number of data points is relatively few.14 If a second or fourth-order polynomial was used to plot the curve the same upward trend in all goods and indicators other than wheat would also be apparent. The wheat data shown in Figure 1 are for private sales and a comparison with sales where the state was involved is shown in Figure 13.

Figure 13
Figure 13

A comparative graph showing the difference between state and private wheat prices in drachmas per aroura from AD 1 to 270.

The variability of state prices is low and it looks as though prices were conventionally set, typically at eight drachmas, rather than established by negotiation and the operation of market forces. This is likely to be related to inequality within the power relationship of buyer and seller. For instance, the state as buyer requisitioned wheat at a price of its choosing. Other forms of state intervention were available other than simple requisitions or sales from public granaries, as in the case shown in P.Oxy. XLII 3048 where in AD 246 the Prefect ordered that all private stocks of wheat in the Oxyrhynchite nome be declared and potentially acquired on behalf of the state at a rate of 24 drachmas. As a major actor in the economy, the state’s pricing position might dampen average prices if it was slower to react to increasing prices than private individuals or generally made purchases at the lower end of the private market price range (Rathbone 1997: 198). Evidence for such behaviour can be seen in Figure 13 above around the beginning of the third century when state prices were maintained at the conventional price of eight drachma whilst private prices generally increased to around 10 to 20 drachmas per artaba.

However, there is another way, other than in their development over time, that prices of wheat seem to differ from other commodities and that is in their numerical format. In any economic sector where prices are determined by supply and demand and there is significant competition in the marketplace, we would expect to see prices whose numerical format reflects the competition between, and among, buyers and sellers. The format of a market price needs to allow for relatively small changes in the marginal pricing of commodities to facilitate offer and bid processes. Therefore in Roman Egyptian terms, for commodities such as barley, wheat, or wine, where the per-unit price was typically under twenty drachmas, it would be an indication of free market activity if prices were expressed in fractions of drachmas, or obols. Such ‘fractional’ pricing is clearly present in wine transactions where many of the prices include obols. Fractional pricing in obols is also present in a number of the barley sources such as P.Louvre I 51 (AD 217–218?). Given the higher per-unit pricing of donkeys and slaves, fractional pricing at the obol level was not necessary to allow market prices to be struck but the prices show sufficient ‘marginal’ variability to allow market processes to function. However, for wheat the pattern is different. Fractional pricing in obols is relatively rare even within private sales, where there are no examples after AD 160 and where prices tend to be expressed in tetradrachm steps such as eight, 12 or 16 drachmas. State wheat pricing exhibits few signs of fractional or market pricing and the vast majority of prices seem conventionally set at eight drachmas. Note that there is little or no evidence for conventional pricing of barley, wine, donkeys, or slaves, other than in the ‘stepping’ of prices in multiples appropriate to the coinage system (Rathbone 1997: 195).

Why do wheat prices show a different pattern?

We have seen that there appears to be a significant difference between the patterns of wheat prices and those for other goods, but what could have caused such variation? What was different about wheat? Firstly, it will be noted that bread made from wheat was the staple element of the diet of the ordinary people of Roman Egypt and thus it had particular social importance. It was also critically a commodity where the state intervened to a greater extent than in relation to other commodities. This state intervention took a number of forms. Taxes or rents from state lands were usually assessed and mostly paid in wheat (Erdkamp 2005: 222). State tenants were frequently supplied with seed loans for wheat but I am not aware of any state loan for other commodities. The greater interest of the state in wheat compared to other goods can be demonstrated by the simple evidence of the number of price points we have for private and state sources for wheat and barley. For wheat, we have a total of 40 private price points within our sample and 31 for the state, so state prices represent 44% of our overall total. For barley, we have a total of 21 private price points and four for the state, so state prices form a much smaller proportion of the admittedly small sample: 16%. These figures support a conclusion that the level of state intervention in wheat transactions was greater than for barley. The absence of state prices for wine or donkeys in our sample would also support the conclusion of greater state interest in wheat than other commodities. To support this interest in wheat there was an ‘organization involving the whole province from local farmers and village granary keepers up to the Procurator Neaspoleos at Alexandria, all tightly under the surveillance of the Prefect of Egypt’ (Rickman 1980: 82).15 Given this extensive state apparatus embedded within key actors in society, I would agree with Rathbone ‘that the wheat market was not entirely free is not surprising’ (Rathbone and von Reden 2014: 189).

Given the lack of evidence for substantial state intervention for barley, wine, and donkeys and the patterns within the prices — where there are marginal pricing, a clear increasing trend over time and no sign of pricing by convention — these commodities may be regarded as goods where ‘exchange-value’ was the dominant feature in the market (Rathbone 1997: 183). What this analysis shows then is a co-existence of two economic sectors, with the prices of wheat being influenced by economic interventions by the state, whilst other commodities were largely left to float to find their own market price. It should be stressed for wheat that this was in no sense an attempt to fix prices as in Diocletian’s Edict. We have no evidence in the period concerned for any central state directives coming from Rome requiring that wheat prices be set at a certain level and there is little evidence for central government grain agents operating at a provincial level (Rickman 1980: 224). This pattern of prices seems rather the result of local state interventions which appear to have had the effect of encouraging wheat production at the expense of other crops. State intervention also seems to have dampened both the level and variability of the average price of wheat, given the policy of state prices being generally lower than private ones at the beginning of the third century and being conventionally set at eight drachmas for the bulk of the period.

Numerical Estimates of Inflation

The discussion above has concentrated on the patterns and shapes of the development of typical prices and indicators, but how would this translate into numerical estimates of inflation as measured by the increase in the price of goods expressed in nominal currency?16 The typical increase rates for individual commodities and indicators can be estimated by examining the best-fit lines for each item. But what general measure of price inflation would be appropriate as a rule of thumb? I have constructed a general ‘blended’ inflation measure that combines the best-fit lines for wheat, barley, wine, and donkeys, and where the weightings given to each line are determined by the number of points in each set.17 The information from the first half of the first century is too sparse to construct an analysis. Note that this blended line is not a price index in the common meaning of a measure that is based on a basket composed of commodities and which reflects the cost of living for a certain type of individual. Constructing such an index is fraught with difficulties and requires knowledge of the consumption patterns of individuals to determine the weighting of individual components within a basket. Allen attempted to construct such a basket for a ‘Mediterranean’ location in the Roman world but relied on data from early modern Northern Europe which he then assumed was appropriate for the Roman period and then further adjusted to a ‘Mediterranean’ location by replacing wine for beer for instance. These assumptions may, of course, be challenged. Another difficulty in attempting to construct a cost of living index for Roman Egypt is that we lack diachronic trend data for significant components such as legumes. It also requires knowledge of how the weighting of different components changed over time, which in turn may be influenced by relative price movements. If, for instance, barley became relatively more expensive compared to wheat, would people have substituted wheat for barley in their shopping ‘basket’?18 Given these difficulties I prefer to adopt the ‘blended’ approach which has the advantage that it does not require any subjective assumptions as to the weighting of each component of the basket and how they changed.19 Whilst by no means perfect, and maybe criticised for the weighting it gives to donkey prices, using the number of observations means that greater weight is given to the components where there is a more robust statistical expectation that the data reflect the experience, and thus, I believe, the line is more likely to reflect ‘reality’.20 The geometric average inflation rate for different commodities and indicators and a blended index, based on the best-fit lines, are shown in Table 1, where it will be noted that the blended index provides a middle-ground estimate of inflation when compared to the individual prices and indicators.

Table 1

A comparative table showing the average percentage increase rates per annum for commodity prices or indicators of price, together with a blended index, for three periods covering AD 50 to AD 270.

Period (AD) Commodities Index Indicators
Wheat Barley Wine Donkeys Blended Donkey Rent Slaves Land Price Land Rent House Price House Rent Loans Earnings
50 to 160 0.4 –0.1 0.4 0.4 0.3 NA21 NA NA 1.0 0.4 0.3 0.7 NA
160 to 190 0.7 0.4 0.6 1.5 0.8 1.4 0.4 0.3 0.6 1.9 0.3 0.5 0.6
190 to 270 0.1 1.4 0.7 1.5 1.1 0.6 0.7 0.6 0.6 1.6 1.1 0.8 1.1

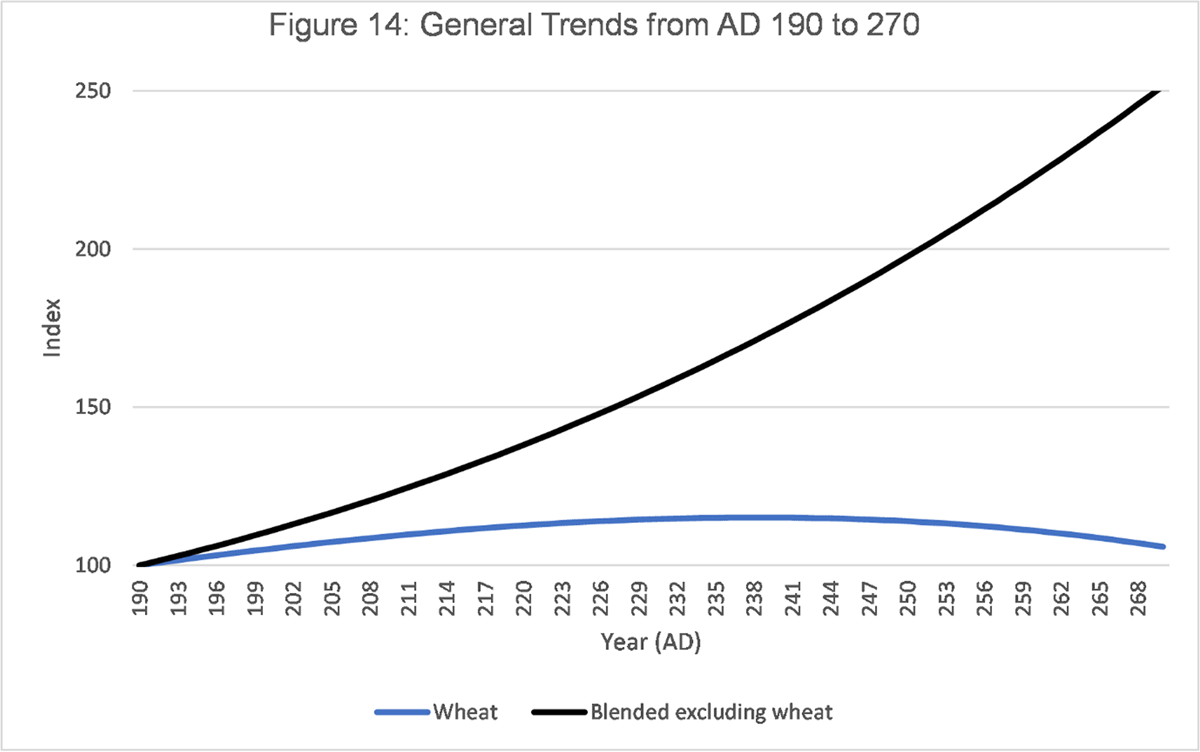
If wheat increases are compared to other items, the clear outlier is the period from AD 190 to 270 when, as we have noted, wheat prices are steady but all the other commodities and indicators continue to show price increases.22 Although the per annum figures appear small, the cumulative effect is significant, as can be seen in Figure 14 when the best-fit line for wheat is compared to a blended best-fit line covering barley, wine, and donkeys.

Figure 14
Figure 14

A comparative graph showing the difference in the third order polynomial best-fit lines for wheat prices and for a blended price index for items other than wheat from AD 190 to 270.

Another feature of note is that earnings appear broadly to keep pace with price inflation as measured by the ‘blended’ index. If a general levelling off of prices truly did occur in the first seventy years of the third century, then the increase in earnings seen would imply a substantial improvement in living standards for ordinary people over that time, which is questionable given the lack of any other evidence for real economic growth during that period.

Conclusions and Implications

Ideally, I would have liked to provide the reader with solid probability likelihoods to test a specific set of propositions as to price trends, including whether prices continued to rise after AD 190, but the limitations of the data and the difficulty of linking trends in prices of goods to other indicators make this impossible to do in a strictly mathematical way. However, 11 out of 12 prices or indicators show increases in the period after AD 190 and I believe it is reasonable therefore to conclude that prices in the period were more likely to have risen than remained steady. The average levels of general price inflation are low in absolute terms, never being much above 1% per annum, and in relative terms are considerably lower than those which have often occurred in modern economies. The differential patterns of wheat prices against other commodities mean that this was an economy where the state influenced the price of the politically and fiscally vital commodity of wheat, but largely left other commodities to find their own level and these two market sectors co-existed. As Rathbone states, a dampening of prices for wheat could have increased demand for other goods, which is consistent with the different patterns seen and the increase in prices for other such goods (Rathbone and von Reden 2014: 188). My view of the price trends for ‘free market’ items in Roman Egypt in the private sector is perhaps a simpler one than that suggested by Rathbone and accepted by Howgego and Scheidel amongst others. There was indeed a period of price stability from around AD 50 to around AD 160, at which point prices started to rise moderately and, prices continued to increase to AD 270, though there will have been periods of shorter-term fluctuations. This conclusion is contrary to the commonly held view that the years from AD 190 to 270 were a period of price stability since the cost of living would have more than doubled over this period. As a rule of thumb, I would suggest that the cost of living in Roman Egypt is assumed to be stable from AD 50 to 150, and that thereafter it increases at an average rate of around 1% per annum up to AD 270.

This regional conclusion has potential implications for a number of important questions relating to the crises that afflicted the whole Empire during the third century. On a microeconomic level, if the evidence above is considered compelling, it requires a reassessment of how ordinary people’s standards of living changed and suggests that wages kept pace with inflation over the period.23 Given the inflationary framework constructed, data from financial transactions over more than 200 years may be ‘normalised’ or ‘re-calibrated’ to a common real value, increasing the usability of this data and allowing direct comparison. An example of the potential that this framework provides would be the quantification of high real returns on investment in land and loans in Roman Egypt, with the resultant implications for wealth concentration (Piketty 2014; Kelly 2020: 230–233). On a macroeconomic level, it provides a framework for considering whether army pay increases in the period were simply inflationary or whether the army took an increasing share of the available resources at others’ expense (for a summary of the debate on the levels of pay and increases see Speidel 2014). Perhaps most importantly, it also contributes to the debate on the effects of coinage debasement on the economy (Haklai-Rotenberg 2011; Bransbourg 2012: 157; Temin 2013: 70–71; Elliott 2020: 126–141).

Finally, as to why the period after the middle of the second century experienced inflationary increases, a detailed analysis of the possible reasons is beyond the scope of this paper. However, in other historical contexts, a plague has led to an inflationary spurt, for instance in mediaeval England after the Black Death, and as Rathbone noted it could well be that the Antonine plague was the trigger for this change (Rathbone 1996: 334; Munro 2005: 11). However, whilst this external event may have been the trigger to start prices increasing, the continued trend over a period of more than one hundred years would point to underlying endogenous systemic economic drivers, linked to fundamental supply and demand issues, which sustained inflation over such a long period.

Supplementary Files

The supplementary files for this article can be found as follows:

Supplementary file 1

Appendix 1, notes on individual commodities and indicators. DOI: https://doi.org/10.16995/traj.4338.s1

Supplementary file 2

Appendix 2, database of prices. DOI: https://doi.org/10.16995/traj.4338.s2

Notes

  1. See Lerouxel 2016: 42 for a similar statement and also Temin 2013: 87–88 for a mathematical proof of price stability after AD 190 but note that he based his corroboration only on wheat prices, and it is thus, I would suggest, flawed. However, he also, based purely on the existence of army pay increases, suggested continued inflation over the third century, Temin 2013: 74. Harper 2016: 816 models two periods of level prices for wheat but sees a ‘sharp increase in price variability across a range of goods and services in the entire period AD 250–275’. However, see Appendix 1 for comments on Harper’s methodology, and thus conclusions, for land prices and rents. [^]
  2. Appendix 1 provides notes on the data concerned and Appendix 2, extracted from the appendices to my doctoral thesis, contains much of the data used. [^]
  3. Bagnall 2011: 74 suggests the inclusion of unpublished papyri inventories to remove some of the bias in the data caused by editorial choice, but time and resources did not allow this process to be undertaken. Ostraca were not included within the wider normative database but were included within the data for prices and indicators when they were identified through the process of review against papyri.info, the published volumes and the lists compiled by previous scholars. [^]
  4. Note however, I did not have access to the unpublished data from the ostraca of the Eastern Desert which contain some prices. Whether it would have been appropriate to include prices of commodities from such a different geographical area given, for instance, the impact of transportation costs, is another matter. [^]
  5. For commodity prices a double check of volumes published after the collections were compiled was undertaken. [^]
  6. If the data for all of Egypt were used for land and house prices then the same pattern of increase would be seen but the data would be more dispersed. [^]
  7. The best-fit line was computed using the least-squares of a general linear model. Note that although a third-order polynomial best-fit curve may exhibit two inflection points, it does not always do so if the data does not warrant this, see Figure 2 for example. For a good description of the use, advantages and limitations of polynomial regression see Aczel & Sounderpandian: 2009: 513–517. Use of a third-order polynomial avoids the need to make subjective choices of dates where prices are believed to have changed in nature, in Harper’s case: AD 160 and the late second century, and thus lets the data show when changes may have occurred without any additional unnecessary assumptions. [^]
  8. I thus consider that the population being analysed is one where documents, rather than price references are the data points. [^]
  9. The data we have available is simply a very small sample of the population of prices that were actually paid in Roman Egypt. Sample bias will arise in a number of ways but by using median prices from each source we ensure that the information given from each source is equally weighted, rather than over-weighting a source with many prices within it and we reduce the likelihood that observations are not independent. However, this bias and dependence cannot be removed entirely since a number of observations are clearly not independent since they come from the same archive or archaeological excavation. [^]
  10. For an excellent summary of the issues relating to their interpretation see Blouin and Burnett 2020: 250–261. [^]
  11. Note that only one of the transactions used in the data refers to the ‘old Ptolemaic’ coins which are referenced in 12 texts from AD 266 (see Kruse and Woytek 2020) and none refer to the ‘new coins’. The case in point is a sale of slave (SPP XX 71, 11–12) and I have retained it as a minimum price in ‘ordinary’ coinage since old Ptolemaic coinage would be likely to have had a higher value as Kruse and Woytek conclude (Kruse and Woytek 2020: 365). [^]
  12. Though I have also examined the log-transformed data for the period after AD 190 to see if the data support an increase in prices after that date. [^]
  13. Though it is not a direct indicator of statistical significance. Note that the charts are not drawn to the same vertical scale but to fit the available space. Differences in the effective rates of increase are listed in Table 1. To be exact, the R2 referred to is the coefficient of determination used with a third-order polynomial via a general linear model. [^]
  14. The data concerned are wheat (R2 = 0.01, n = 27), barley (R2 = 0.61, n = 10), donkeys (R2 = 0.25, n = 14), slaves (R2 = 0.48, n = 8), wine (R2 = 0.18, n = 40). I could expand on these statistics to attempt to make conclusions as to statistical likelihoods (see Temin 2013: 86–88 who did so solely for wheat), but I cannot combine evidence from commodities and indicators in a rigorous way to come to a statistically valid conclusion as to prices overall. [^]
  15. The authorities monitored wheat prices right up until the end of the Empire (Bransbourg 2012: 92). This is not to say that there was no state involvement in the market for commodities other than wheat. The state did require, and on occasion, requisition donkeys, barley and wine for military and civilian purposes. For example, PSI X 1123 (AD 152) shows the state requisitioning wine for Alexandria from the Oxyrhynchite nome, but the extent of this intervention was less than that for wheat. [^]
  16. Inflation could of course also be construed to include the costs of services and housing, but for simplicity, the remainder of this section relates to assessing how prices of goods may have increased. [^]
  17. The process of blending the data was as follows. The best-fit lines for each good were re-based to have a starting index of 100 at AD 50. This produces a range of comparable values for each year to AD 270. For any year the blended index value is the arithmetic average of the values for the individual goods, weighted by the number of observations. [^]
  18. Though I have also constructed traditional indices based on Allen’s Mediterranean ‘respectability’ and ‘bare bones’ indices. The resulting inflation rates are essentially the same as the ‘blended’ index for the period to AD 190, but for the period from AD 190 to AD 270, the per annum rates are 0.9% and 0.7% respectively compared to the 1.1% ‘blended’ index rate shown in Table 2. See Allen 2009, where it should be noted that in the summation of the cost of the Mediterranean Respectability basket (Allen 2009: 334) there is a mathematical error as the total sum should amount to c.232 rather than 163.921 as quoted by Allen. [^]
  19. Mathematically it is equivalent to constructing a basket of goods where the weighting given to each component is equal to the proportion of data points represented by that component. [^]
  20. An alternative approach could be to give equal weighting to each commodity as a component of the index, but this would ignore the quality of the information provided. Imagine if you had two commodities x and y, where for x you had two data points separated by 200 years and for y had 100 evenly spread over the period. If you weigh both of these equally you are giving equal credence to both sets of data whereas the quality of information is much better for y than for x. [^]
  21. There are too few data points for any conclusion to be drawn on donkey rents, slave prices, land prices or earnings in the period from AD 50 to 160. [^]
  22. Note that if straight-line best-fit lines were constructed for the period AD 190 to AD 270 using just data from this period, then all commodities and indicators other than wheat show upward price trends. The average inflation rates for those items where there is sufficient data for a rate to be calculated, that is barley, donkeys, wine, fodder rents and loan sizes, are within 0.2% of the figures shown in Table 1. [^]
  23. For instance, Scheidel 2010 assumed that from the 190s to the early 270s AD prices of goods were level within fairly narrow bands which appears inappropriate. [^]

Acknowledgements

I would particularly like to thank Professor Rathbone, not only for his guidance and expertise without which this paper would not have been possible but also for his openness to alternative interpretations of the data.

Funding Information

This research was undertaken when the author was in receipt of an AHRC/LAHP grant for his doctoral thesis.

Competing Interests

The author has no competing interests to declare.

References

Aczel, A.D. and Sounderpandian, J. 2009. Complete Business Statistics (7th edition). New York: McGraw-Hill/Irwin.

Allen, R.C. 2009. How prosperous were the Romans?: evidence from Diocletian’s Price Edict (AD 301). In: A. Bowman and A. Wilson (eds) Quantifying the Roman Economy: Methods and Problems. Oxford: Oxford University Press: 327–345. DOI:  http://doi.org/10.1093/acprof:oso/9780199562596.003.0016

Bagnall, R.S. 1985. Currency and Inflation in Fourth Century Egypt. Chico: Scholars Press.

Bagnall, R.S. 2011. Everyday Writing in the Graeco-Roman East. Berkeley: University of California Press. DOI:  http://doi.org/10.1525/california/9780520267022.001.0001

Bagnall, R.S. and Bransbourg, G. 2020. The Constantian monetary revolution. In: T. Faucher (ed.) Money Rules! The Monetary Economy of Egypt, From Persians until the Beginning of Islam. Cairo: Institut Français d’Archéologie Orientale: 367–392.

Blouin, K. and Burnett, A. 2020. From kings to emperors. The development and integration of the Egyptian monetary system into the Roman Empire. In: T. Faucher (ed.) Money Rules! The Monetary Economy of Egypt, From Persians until the Beginning of Islam. Cairo: Institut Français d’Archéologie Orientale: 231–286.

Bogaert, R. 2000. Les opérations des banques de l’Égypte romaine. Ancient Society 30: 135–269. DOI:  http://doi.org/10.2143/AS.30.0.565562

Bransbourg, G. 2012. Rome and the Economic Integration of Empire. Available at http://doi.org/2333.1/280gb73f [Last accessed 22 February 2021].

Cuvigny, H. and Lach-Urgacz, K. 2020. ’ρεινὸν κέρμα. Monetary circulation in the Praesidia of the Eastern Desert during the Principate. In: T. Faucher (ed.) Money Rules! The Monetary Economy of Egypt, From Persians until the Beginning of Islam. Cairo: Institut Français d’Archéologie Orientale: 309–341.

Drexhage, H.-J. 1991. Preise, Mieten, Pachten, Kosten und Löhne im römischen Ägypten bis zum Regierungsantritt Diokletians. St. Katharinen: Scripta Mercaturae.

Duncan-Jones, R.P. 1994. Money and Government in the Roman Empire. Cambridge: Cambridge University Press. DOI:  http://doi.org/10.1017/CBO9780511552632

Elliott, C.P. 2020. Economic Theory and the Roman Monetary Economy. Cambridge: Cambridge University Press. DOI:  http://doi.org/10.1017/9781108290531

Exner, J.E. 2002. The Rorschach: Basic Foundations and Principles of Interpretation: Volume 1. Hoboken: Wiley.

Erdkamp, P. 2005. The Grain Market in the Roman Empire: A Social, Political and Economic Study. Cambridge: Cambridge University Press. DOI:  http://doi.org/10.1017/CBO9780511482755

Gendy, I. 1990. Economic Aspects of Houses and Housing in Roman Egypt. Unpublished thesis (PhD), University College London.

Haklai-Rotenberg, M. 2011. Aurelian’s monetary reforms: between debasement and public trust. Chiron 41: 1–39.

Harper, K. 2016. People, plagues, and prices in the Roman world: the evidence from Egypt. Journal of Economic History 76: 803–39. DOI:  http://doi.org/10.1017/S0022050716000826

Hennig, D. 1967. Untersuchungen zur Bodenpacht im ptolemäisch-römischen Ägypten. Munich: R. Habelt.

Herrmann, J. 1958. Studien zur Bodenpacht im Recht der graeco-aegyptischen Papyri. Munich: Beck.

Howgego, C., Butcher, K., Ponting, M., and Heuchert, V. 2010. Coinage and the Roman Economy in the Antonine Period: The View from Egypt. Available at http://oxrep.classics.ox.ac.uk/docs/Howgego2010.pdf [Last accessed 26 August 2020].

Johnson, A.C. 1936. Roman Egypt to the Reign of Diocletian. (An Economic Survey of Ancient Rome, ed. by T. Frank, vol. II.). Baltimore: The John Hopkins Press.

Kelly, P.V. 2020. Risk and Return in Roman Egypt. Were Markets in Roman Egypt Driven by Financial Rationality? Unpublished thesis (PhD), King’s College London.

Kruit, N. and Worp, K.A. 1999. Metrological notes on measures and containers of liquids in Graeco-Roman and Byzantine Egypt. Archiv für Papyrusforschung und verwandte Gebiete 45: 96–127. DOI:  http://doi.org/10.1515/apf.1999.45.1.96

Kruse, T. and Woytek, B.E. 2020. “(Old) Ptolemaic” and “new” coins in 3rd-century AD Egypt. A reassessment of the papyrological and numismatic evidence. In: T. Faucher (ed.) Money Rules! The Monetary Economy of Egypt, From Persians until the Beginning of Islam. Cairo: Institut Français d’Archéologie Orientale: 341–366.

Kutzner, E. 1989. Untersuchungen zur Stellung der Frau im römischen Oxyrhynchos. Frankfurt: P. Lang.

Lerouxel, F. 2016. Le marché du crédit dans le monde romain (Égypte et Campanie). Rome: École française de Rome.

Maehler, H. 1983. Hauser und ihre Bewohner im Fayum in der Kaiserzeit. In: G. Grimm et al. (eds) Das römisch-byzantinische Ägypten: Akten des internationalen Symposions 26– 30. September 1978 in Trier. Mainz: P. von Zabern: 119–38.

Masciadri, M.M. and Montevecchi, O. 1984. I contratti di baliatico. Milan: Tibiletti.

Mickwitz, G. 1932. Geld und Wirtschaft im römischen Reich des vierten Jahrhunderts n. Chr. Leipzig: Harrasowitz.

Montevecchi, O. 1941. Ricerche di sociologia nei documenti dell‘Egitto greco-romano. III. – I contratti di compra-vendita. Aegyptus 21: 93–151.

Montevecchi, O. 1943. Ricerche di sociologia nei documenti dell’Egitto greco-romano: III. – I contratti di compra-vendita. Aegyptus 23: 11–89.

Munro, J. 2005. Before and After the Black Death: Money, Prices, and Wages in Fourteenth-Century England, 15 December 2004. Available at https://ideas.repec.org/p/tor/tecipa/munro-04-04.html [Last accessed 26 August 2020].

Piketty, T. 2014. Capital in the Twenty-First Century. Cambridge: The Belknap Press of Harvard University Press. DOI:  http://doi.org/10.4159/9780674369542

Rathbone, D. 1996. Monetization, not price-inflation, in third-century AD Egypt?. In: C.E. King and D.G. Wiggs (eds) Coin Finds and Coin Use in the Roman World. Berlin: Gebr.Mann Verlag GmbH & Co KG: 321–339.

Rathbone, D. 1997. Prices and price formation in Roman Egypt. In: J. Andreau, P. Briant, and R. Descat (eds) Économie antique: prix et formation des prix dans les économies antiques. Saint-Bernard-de-Comminges: Musée archéologique départemental: 183–244.

Rathbone, D. and von Reden, S. 2014. Mediterranean grain prices in classical antiquity. In: R.J. Van der Spek, J. Luiten van Zanden, and B. van Leeuwen (eds) A History of Market Performance: From Ancient Babylonia to the Modern World. Abingdon: Routledge: 148–235.

Rickman, G.E. 1980. The Corn Supply of Ancient Rome. Oxford: Oxford University Press.

Rowlandson, J. 1996. Landowners and Tenants in Roman Egypt: The Social Relations of Agriculture in the Oxyrhynchite Nome. Oxford: Clarendon Press.

Scheidel, W. 2010. Real wages in early economies: evidence for living standards from 1800 BCE to 1300 CE. Journal of the Economic and Social History of the Orient 53: 425–462. DOI:  http://doi.org/10.1163/156852010X506038

Speidel, M.A. 2014. Roman army pay scales revisited: responses and answers. In: M. Reddé (ed.) De l’or pour les braves ! – Soldes, armées et circulation monétaire dans le monde romain. Bordeaux: Ausonius: 53–62.

Temin, P. 2013. The Roman Market Economy. Princeton: Princeton University Press. DOI:  http://doi.org/10.23943/princeton/9780691147680.001.0001

Tenger, B. 1993. Die Verschuldung im romischen Aegypten (1.–2. Jh. n. Chr). St. Katharinen: Scripta Mercaturae Verlag.

van Minnen, P. 2009. The future of papyrology. In: R.S. Bagnall (ed.) The Oxford Handbook of Papyrology. Oxford: Oxford University Press: 644–660.